1.1.2 原點放大縮小(scaling)

對於某些點座標若需進行比例放大或縮小，其影響在特性矩陣中，正好是對角線之元素位置，而放大比例依其放大係數S值而定。故S值可以分為在各座標方向如ｘ與ｙ之分別放大量。在A轉換特性矩陣中，其對角元素均為一，若要進行放大縮小則需改變對角項1的位值。因此，只要將對應之１值改為S之對應值Sx, Sy(或Sz)即可;而最後一個1則維持原狀不變化，即：

二維：

  x' = (Sx) x
  y' = (Sy) y    ----1.12

 [A] = [Sx  0  0
        0   Sy 0
        0   0  1 ]----1.13

三維：

  x' = (Sx) x
  y' = (Sy) y
  z' = (Sz) z  ----1.14

 [A] = [Sx  0  0  0
        0   Sy 0  0
        0   0  Sz 0
        0   0  0  1 ]----1.15

由 12式及14式可知，座標值之放大縮小實際上只要將其對應之座標各乘以對應之Ｓｘ，Ｓｙ，Ｓｚ即可，在正常的運算上也可如此做。例如：有四個空間點之座標需各放大為[0.5 1 2] 倍：

>>x=[2 3 4 5];y=[-1 2 -4 5];z=[10 24 30 5];
>>X=x*0.5; Y=y*1; Z=z*2;
>> X
X =
    1.0000    1.5000    2.0000    2.5000
>> Y
Y =
    -1     2    -4     5
>> Z
Z =
    20    48    60    10

利用MATLAB指令執行結果如上述。
若要採用一致性的矩陣表示法，亦可採用第13及 15式之矩陣相乘之型式，此時可令[C]=[x y z 1]及[C']=[x' y' z' 1]，代入公式1.8即可求得對應之放大值。

　　[C'] = [C][A]---------------1.8

利用MATLAB程式函數trans4E(c,S)可以完成放大縮小之應用，此時之輸入倍數則以factor表示，其程式內容如下：

function xprime=trans4E(C, factor)
%
%function xprime=trans4E(C,factor)
%To scale up & down the coordinates by a factor
%Inputs:
%  C: the matrix to be transformed,[x y] or [x y z]
%  factor: scaling ratio, [sx sy] or [sx sy sz]
%  xprime: resultant matrix transformed
% Example: xprime=trans4T([2 3 4],[0.1 0.2 0.3])
%Author: D.S. Fon, Bime, NTU, Date: Nov.20,2004
[n,m]=size(C);
if length(factor)~=m,
  disp('The dimension is inconsistent!');
  xprime=[];return;
end
C=[C,ones(n,1)];
A=eye(m+1); A(m+1,:)=[factor 1];
xx=C*A;xprime=xx(:,1:m);

實例：

>> trans4E([3 5 1],[2 2 2])
ans =
   6    10     2

其結果與3*2=6, 5*2=10, 1*2=2的運算相同。
實例：多點作放大時，其結果如下述。

>> c1=[0 0;1 3;4 2;0 0]
c1 =  0     0
   1     3
   4     2
   0     0
>> line(c1(:,1),c1(:,2))
>> c2=trans4E(c1,[2 3])
c2 =  0     0
   2     9
   8     6
   0     0
>> line(c2(:,1),c2(:,2))
>>grid on

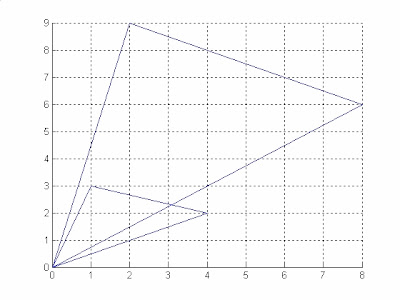
圖1.2 座標之放大與縮小