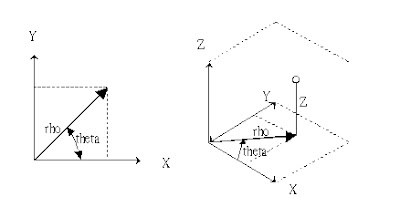
若將速度量再對時間t微分則為加速度A,即:
A=dV/dt=d/dt(r'ejθ+jrθ'ejθ)
=[(r"+jr'θ')+(jr'θ'+jrθ"-rθ'²)]ejθ
=[(r"-rω²)+j(2r'ω+rα)]ejθ
=[(r"-rω²)+j(2r'ω+rα)](cosθ+jsinθ)
=[(r"-rω²)cosθ-(2r'ω+rα)sinθ)]-...
j[(r"-rω²)sinθ+(2r'ω+rα)cosθ]-----------(3.21)
3.6.1加速度公式
上式若桿長為固定時,即 r'=0,則上式可簡化為:
A=dV/dt=d/dt(jrθ'ejθ)
=[(-rω²)+jrα]ejθ
=[-rω²+jrα](cosθ+jsinθ)
=[-rω²cosθ+rαsinθ)]+j[-rω²sinθ+rαcosθ]---(3.22)
若就圖2之轉換象限之觀念而言,上式加速度亦可改變如下:
A=-rω²ejθ+jrαejθ
= rω²(j²ejθ)+rα(jejθ)
= rω²ej(θ+π)+rα(jej(θ+π/2))---(3.23)
加速度向量具有二兩項分項量,一為指向負的徑向(相差180度),即為向心加速度;一為指向切線方向,成90度方向,與速度相同。
3.6.2 MATLAB加速度函數
任何連桿運動時,均會產生加速度,其值之計算則可利用Matlab函數acc2.m。此函數之輸入項包括各桿之長度(rho)、水平角度(theta)、對應之角速度(omega)及角加速度(alfa)。輸出則為絕對值與合成桿之夾角。每項內有三元素分別說明位置、速度及加速度之向量。
acc2.m程式中,係採用複數表示法計算位移、速度及加速度量。輸入項中若僅輸入前兩項,則角速度設為一單位,若僅三項則角加速度設為零。連桿數則可以無限。
function [sv,thetap]=acc2(rho,theta,omega,alfa)
% Find the acceleration Ap for the
% connecting vectors with theta,rho,omega & alfa
% theta: angle in degrees for each vector
% rho: radial displacement
% omega: angular velocity of each vector
% alfa: angular accerlation of each vector
% Example:
%[sv,th]=acc2([5 8 9],[10 135 12],[10 20 30],[5 10 20])
theta=theta(:);rho=rho(:);
n=length(rho);
%handling the default values
if nargin<4,
alfa=zeros(size(rho));
if nargin==2,
omega=ones(size(rho));
end
end
if length(omega)==1,omega=ones(size(rho))*omega;end
if length(alfa)==1,alfa=ones(size(rho))*alfa;end
%
omega=omega(:);alfa=alfa(:);
d2g=pi/180; %轉換為弧度
xtheta=exp(i*theta*d2g);
ss=rho.*xtheta;
vv=i*rho.*xtheta.*omega; %將極座標換為複數座標
aa=(-rho.*omega.^2+i*rho.*alfa).*xtheta; %將極座標換為複數座標
sp=sum(ss);vp=sum(vv);ap=sum(aa); %行矩陣之加總
sv=[abs(sp) abs(vp) abs(ap)];%位移與速度之絕對值
thetap=[angle(sp) angle(vp) angle(ap)]/d2g;%位移與速度之相角,並轉回一般角度
執行例1:僅有一桿,其長度為5公分,角速度為10rad/s,角加速度為20rad/s²,則執行結果如下:
>> [sv,th]=acc2(5,10,20)
sv =
5 100 2000
th =
10 100 -170
結果其位移量仍為5cm,絕對速度為100cm/s,絕對加速度為2000cm/s²。其對應角度方面,位移仍維持原有之10度,絕對速度之位角為100度,與前者相差正好90度;絕對加度之相差為-170度,與原位移相差正好180度。
執行例2:若有三桿,其位置向量分別為[5 8 9]cm,對應位移角度為[10 135 12]度;角速度分別為10, 20, 30 rad/s,無角加速度,求三桿合併後之總運動狀態。
>> [sv,th]=acc2([5 8 9],[10 135 12],[10 20 30])
sv =
11.646 267.86 7357
th =
46.133 131.63 -146.75
執行例3:同前例,但各桿之角加速度均為3rad/s²,求三桿合併速度及加速度。
>> [sv,th]=acc2([5 8 9],[10 135 12],[10 20 30],3)
sv =
11.646 267.86 7364.9
th =
46.133 131.63 -147.02
3.6.3 應用實例
多桿連結之分析
多桿連結是一個開放型機構,故其端點之位置完全依各桿之長度與角度。實際上其分析仍然依位置、速度及加速度等三種項量加以整合。但在速度與加速度的場合必須有各桿之角度、角速度及角加速度之參數,才獲得整合的答案。當然有些情況可以讓其中一個桿之輸入參數變化,其餘保留為定數,因而可以瞭解某特定桿變動時對整個機構之影響。多桿連結分析在工程機械上應用較多,如怪手、機器人等均屬此類。
下面的MATLAB程式dyad(),其呼叫語法如下:
function [vec, dyadata] = dyad(rho,theta,td,tdd)
讀者不妨自行執行後,觀察其結果。左邊之輸出參數中,vec為位置,速度及加速度之絕對值及其對應水平角度;dyadata則為各桿之對應值。
function [vec,dyadata] = dyad(rho,theta,td,tdd)
%
% function [vec, th, dyadata] = dyad(rho,theta,td,tdd)
% Analyzes a dyad linkage composing a crank and a dyad.
% Inputs: rho:length of links
% theta:incling angles, deg.
% td:angular velocity, rad/s
% tdd:angular acceleration, rad/s^2
% Outputs: vec:absoute length of links
% dyadata:original data, in complex forms
% Example:[vec,dyadata] = dyad([5 10],[30 50],[2 4])
theta=theta(:);rho=rho(:);
n=length(rho);
if nargin<4,
tdd=zeros(size(rho));
if nargin==2,
td=ones(size(rho));
end
end
if length(td)==1,td=ones(size(rho))*td;end
if length(tdd)==1,tdd=ones(size(rho))*tdd;end
td=td(:);tdd=tdd(:);
d2g=pi/180;
tt=exp(i*theta*d2g);
pp=rho.*tt;vv=i*td.*pp;aa=-pp.*td.^2+i*pp.*tdd;
dyadata=[pp vv aa];
vec=[abs(sum(dyadata));angle(sum(dyadata))/d2g];
執行範例:
>> [vec, dyadata] = dyad([5 10],[30 50],[2 4])
vec =
14.7976 49.5152 178.9247
43.3637 136.0392 -132.1910
dyadata =
1.0e+002 *
0.0433 + 0.0250i -0.0500 + 0.0866i -0.1732 - 0.1000i
0.0643 + 0.0766i -0.3064 + 0.2571i -1.0285 - 1.2257i
如何利用上面dyad函數程式可以用來計算相關連桿之速度與加速度,然後進行繪圖。此時亦須應用到第二章介紹之 linkshape函數,以繪出一般連桿之外形。下面的程式dyad_draw先呼叫dyad取得相關資料,再利用 linkshape繪製。linkshape函數附於此程式之後,可以隨時呼叫。程式內容如下:
function dyad_draw(rho,theta,td,tdd)
% Call function dyad(rho,theta,td,tdd) to
% analyze a dyad linkage composing cranks and a dyad with drawing.
% Inputs: rho:length of links
% theta:incling angles, deg.
% td:angular velocity, rad/s
% tdd:angular acceleration, rad/s^2
% Example:
% dyad_draw([15 10 5],[0 60 90],[.5 .8 .5],0)
clf;
[vec,data] = dyad(rho,theta,td,tdd);
x=[0;cumsum(real(data(:,1)))];y=[0;cumsum(imag(data(:,1)))];
for i=1:length(x)-1
linkshape([x(i) y(i)],[x(i+1) y(i+1)],1);
end
for k=1:length(rho)
x0=x(k+1);y0=y(k+1);
vx=x0+real(data(k,2));vy=y0+imag(data(k,2));
ax=x0+real(data(k,3));ay=y0+imag(data(k,3));
line([x0 vx],[y0 vy],'marker','s','linewidth',2);
line([x0 ax],[y0 ay],'marker','s','color','r','linewidth',3)
end
sdata=sum(data);
ss=[real(sdata(1)) imag(sdata(1))];
vv=[real(sdata(2)) imag(sdata(2))];
aa=[real(sdata(3)) imag(sdata(3))];
line([0 ss(1)],[0 ss(2)],'linestyle',':','linewidth',2)
line([ss(1) ss(1)+vv(1)],[ss(2) ss(2)+vv(2)],...
'marker','d','color','g','linewidth',3)
line([ss(1) ss(1)+aa(1)],[ss(2) ss(2)+aa(2)],...
'marker','d','color','m','linewidth',3)
axis equal;grid on
function linkshape(A,B,dd)
% Draw a link
% Inputs:
% A,B:Initial & final coordinates of link
% d:thickness of link(negative for line link)
% Example: linkshape([0 0],[5,5])
if nargin==2,dd=1;end;
d=abs(dd);
AB=(B(1)+j*B(2))-(A(1)+j*A(2));
D=abs(AB);th=angle(AB);
t=linspace(pi/2,2.5*pi,20);
Cout=max(d/2,0.2)*exp(j*t');Cin=Cout/2;
if dd>0,
P=[0;Cin;Cout(1:10);D+Cout(11:20);D+Cin;D+Cout(20);Cout(1)];
else
P=[Cin;0;D;D+Cin];
end
xx=real(P);yy=imag(P);
x=xx*cos(th)-yy*sin(th)+A(1);
y=xx*sin(th)+yy*cos(th)+A(2);
line(x,y)
axis equal
執行例:
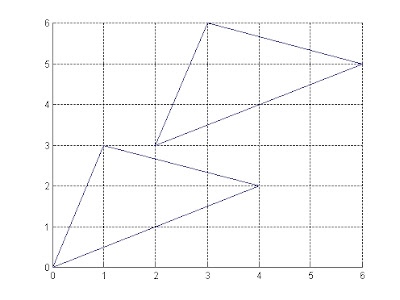
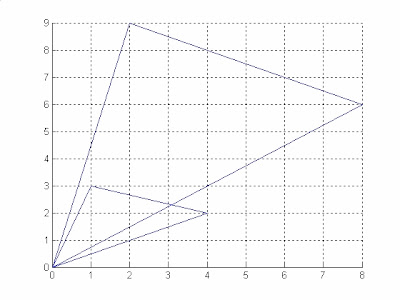
設有三桿相連結成端桿之型式。各桿之長度分別為[15 10 5]cm,[0 60 90]度,[.5 .8 .5]rad/s^2。設各桿之角加速度為0,利用上面之函數執行如下:
dyad_draw([15 10 5],[0 60 90],[.5 .8 .5],0)
其結果如下:
 其中之紅色為各桿之加速度,藍色為速度,綠色為合速度
其中之紅色為各桿之加速度,藍色為速度,綠色為合速度