1.1.1 平移(Translation)

平移是沿x軸或y軸方向分別平移Tx、Ty之量，換言之，經過平移後之新座標x'，y'應有下列的關係：

   x'= x + Tx
　 y'= y + Ty---------1.5

由此一聯立方程式可知，在運算上，只要將(x,y)之對應座標值分別加上Tx,Ty即可，例如：
若有座標點A,B,C,D分別為(2,4),(3,9),(4,16),(5,25)，則在MATLAB中，可以將其分成兩組對應之座標值(x,y)，則用列矩陣表示如下：

>> x=[2 3 4 5]
x =
     2     3     4     5
>> y=[4 9 16 25]
y =
     4     9    16    25

這兩組座標是對應的，屬於二維之座標。故若要將此組座標分別移(5,10)之距離，則可以就x,y組合之座標值處理如下：

>> x=x+5
x =
     7     8     9    10
>> y=y+10
y =
    14    19    26    35

兩組座標顯然分別加上各別的距離(5,10)。

然而在矩陣的表示法中，有時候反而比較麻煩，然而利用矩陣卻能將座標之轉移，作成特定的格式，放諸四海而皆準，故也有其特殊的意義。因此，配合公式2.3，可以得到下面類似型式：

　[x' y' 1] = [x y 1] [1  0  0
                      0  1  0
                      Tx Ty 1 ]-----1.6

公式2.6之最後矩陣稱為轉換矩陣，若以Ａ表示，則：

[A] = [1  0  0
      0  1  0
      Tx Ty 1 ]----1.7

設原座標矩陣[Ｃ]= [ x y 1 ]及轉換後之座標矩陣[C’]= [x' y' 1]分別代表轉換之列矩陣值，則：

[C'] = [C] [A] ------1.8

式中，

[C]  = [x  y  1]
[C'] = [x' y' 1]

同理，由公式1.4得知：三維之平移轉換方程式為：

x' = x + Tx
y' = y + Ty
z' = z + Tz -------------1.9

利用相同的觀念，實際上亦可以將三維座標分成三部份，然後就其各部份加上特定係數，終會獲得結果。但同樣，利用矩陣相乘的模式，亦可處理三維座標值之平移的型式，因此其相對之平移轉換矩陣型式可以改寫如下：

[x' y' z' 1]=[x y z 1][1  0  0  0
                  　   0  1  0  0
                 　    0  0  1  0
               　      Tx Ty Tz 1 ]-------  1.10

在等式之右側為原來之座標系與一方型矩陣相乘，此轉換矩陣A即為：

[A] = [1  0  0  0
    　 0  1  0  0
  　   0  0  1  0
  　   Tx Ty Tz 1 ]------1.11

設原座標矩陣[Ｃ] = [ x y z 1]及轉換後之座標矩陣[C’] = [ x' y' z' 1]，分別代表轉換之列矩陣值。則其關係為Ｃ'＝ＣＡ。

將上述的關係寫成MATLAB之函數，其程式如下：

程式：

function xprime=trans4T(C, T)
%
%function xprime=trans4T(C,T)
%To transform the translational coordinates
%Inputs:
%  C: the row matrix to be transformed
%  T: increment of transformation [Tx Ty Tz]
%  xprime: resultant matrix transformed
% Example: xprime=trans4T([2 3 4],[2 4 6])
%Author: DS Fon, Bime, NTU, Date: Jan. 22,2007
[n,m]=size(C);
if length(T)~=m,
  disp('The dimension is inconsistent!');
  xprime=[];
  return;
end
C=[C,ones(n,1)];
A=eye(m+1); 
A(m+1,:)=[T 1];
xx=C*A;xprime=xx(:,1:m);
%%%%%%%%%%%%%%%%%%%%%%%%

初次碰上這種程式者，可能要由程式之寫作過程上另外加把勁，但寫程式重在其邏輯思路，除熟悉指令內容外，必須將每一步驟之思路想通才行。這個程式很短，凡是程式行前面加上％者，都是註釋行，程式是不執行的，所以只當作程式說明而已。所以真正程式本身，才十來行而已。記得在執行MATLAB程式寫作時，每一個變數是以矩陣看得，所以其代表的至少為1X1的矩陣。

以上面的例子，C可能為一群座標點，它可能代表數千點的座標點，但執行時，卻可以將整體座標同時改變。MATLAB程式函數trans4T(c,T)之功能可以完成上項應用在平移的情況。

實例一：

>> trans4T([3 5 1],[2 2 2])
ans =
5     7     3

其如果與3+2=5, 5+2=7, 1+2=3之情況相同。事實上如果僅這麼簡單，那何必動刀動槍，如此大費週章？問題是大部份的例子並不如此簡單，正如前文所述，第一項的輸入值往往不僅代表這樣的一點座標而已。

實例二：設c1為一個三角形之三個頂點座標組成，繪出三角形時，必須採用連連看的方法，由起點開始，逐點連線，最後還要連回起點，故座標點應有四點才能連出一個三角形。

>> c1=[0 0;1 3;4 2;0 0]
c1 =
0     0
1     3
4     2
0     0
>> line(c1(:,1),c1(:,2)) %這是連線的指令，其第一項需為X座標第二項為Y座標。
>>c2=trans4T(c1,[2 3])　%將原來的點移動一個距離。
c2 =
2     3
3     6
6     5
2     3
>> line(c2(:,1),c2(:,2))　%再次繪出移動後之三角形。
>> grid on　%設定為格線。

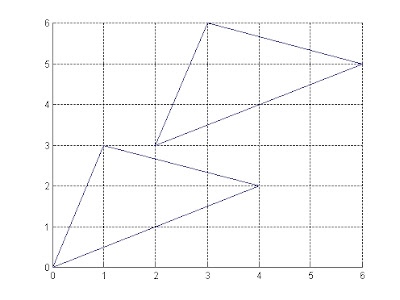
圖2.1 座標之平移

函數tans4T()因而可以平移各點，並據以繪圖。特別注意的函數中間的參數Ｃ是多維向量，其行數依二維或三維而定，不能混用。Line(x,y)則為繪直線函數，可依x,y之對應值作點間連線。