具有動滾動接觸面之連桿,其迴路向量則必須先通過該桿之圓心再與其他連桿相連。這種情況以凸輪、摩擦輪、皮帶輪或齒輪之情況,在分析齒輪組間之驅動時通常僅考慮為節圓接觸,因此無論其所採用之齒型如何,在大觀分析上齒輪動力傳遞仍以節圓為準。
兩節圓相接觸時,除瞬時所產生之迴路外,尚需考慮其滾動接觸的轉動關係,此稱為滾動接觸方程式。利用接觸時之滾動關係才能配合迴路向量之方程式進行解題。茲就節圓之接觸方式分別討論如下:
一、外接圓滾動
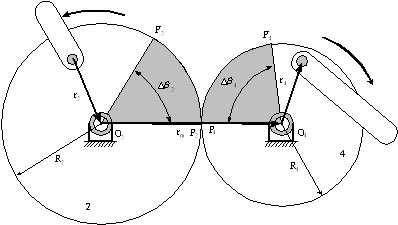
圖9.1 兩圓型連桿件滾動接觸時之情形
由圖9之兩滾動接觸圓之得知,其迴轉角度之關係如下:
R2θ2= -R4∆θ4
其中之負號表示迴轉的方向相反。而 兩角度量則是考慮轉動之起始與終點間之增量,故若整個機構(或此連桿組)本身亦具有系統迴轉量時,上述之角度量亦必須扣除系統迴轉量。設其迴轉量為∆θ5 ,則可修正上述關係如下:
R2(∆θ2-∆θ5)= -R4(∆θ4-∆θ5)
若考慮個別之初始角度與最終角度,即:
∆θ2=θ2-θ2i
∆θ4=θ4-θ4i
∆θ5=θ5-θ5i
代入上式,則公式可整理如下:
(θ2-θ2i)+(R4/R2)(θ4-θ4i)=[1+(R4/R2)(θ5-θ5i)]
此即為外接圓滾動接觸方程式。
二、內接圓滾動
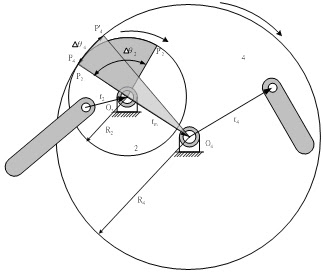
圖9.2 內接圓滾動接觸時之情形
內接圓之滾動是其中一個圓在另一圓之內部滾動,此時之基本公式可由上面導出,只是因為兩圓之轉動方向相同的緣故,其符號將有所改變,如:
R2θ2= R4∆θ4
(θ2-θ2i)-(R4/R2)(θ4-θ4i)=[1+(R4/R2)(θS-θSi)]
三、直線滾動
小齒輪與齒條之組件即為一個外節圓與一直線平面接觸滾動的例子。圖11所示為初始位置當節圓在一平台上滾動時之相關位置,經過滾動一段距離後加上整個組合可能之轉動,可以得到如圖11b之位置。在轉動之過程中,O2P2與O4P4永遠垂直,故其迴轉之角度θS間之關係如下:
R2(∆θ2-∆θ5)= ∆r
代入初始角度,得:
(θ2-θ2i)-(θ4-θ4i)/R2=θ5-θ5i
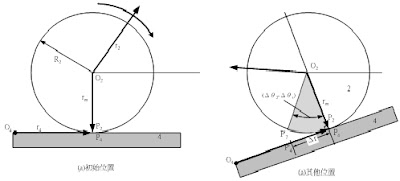
圖9.3 直線滾動之變化情形
範例7.1
某包含一組齒輪之五連桿如圖7.6,其齒輪2與4之直徑分別為6、7cm。其他桿之相關尺寸為r1=8cm,r5=6cm。齒輪2為驅動輪。在初始位置時ABC正好成一直線,設桿2角度之初始值為零。試分析當桿2旋轉60度角時,其他相關之θ3、θ4、θ5值各為如何?
 圖7.6
圖7.6[解]:
這是有一組相互以連桿AB就圓心相連,但兩圓相互間作滾動的例子。雖然桿五與圓4在C點以旋轉結相連,但由於連桿AB之關係,使圓2與圓4不但會自行滾動,而且會依AB軸作轉動。因此,參考書中公式7.6之關係仍然維持。解題時可依下列過程進行:
1. 先就圖7.6(a)建立r3、r4、r5、r1等四桿間之向量關係,並在X-Y座標內建立方程式如下:
r3 + r4 = r5 + r1 7.11
圖7.6 範例7.1之初始位置及相關位置
r3cosθ3 + r4cosθ4 - r5cosθ5 - r1 = 0 (7.12)
r3sinθ3 + r4sinθ4 - r5sinθ5 =0 (7.13)
2. 通常初始位置選在bc桿成一直線時(圖7.6(b)),即 (兩者均為初始值),代入上式,得:
(r3 + r4)cosθ30 -r5cosθ50 = r1 (7.14)
(r3 + r4)sinθ30 -r5sinθ50 = 0 (7.15)
欲求得初始位置之對應角度θ30,θ50可先利用餘弦定理,求得θ50,即
(r3 + r4)² = r1²+r5²- 2r1r5cos²(π-θ50) (7.16)
cos(θ50)= {(r3 + r4)²-r1²-r5² }/(2r1r5) (7.17)
將7.17式代入7.14式後,可得另一個角度之餘弦:
cos(θ30)=(r1 + r5cosθ50)/(r1+r4) (7.18)
下面為利用MATLAB撰寫之程式函式f5link_int(),以計算桿3及桿5之初始角度,其呼叫型式為:
function [th3,th4,th5]=f5link_int(r)
其輸入項為r。其中包括五桿之長度,其中第二桿為驅動齒輪之半徑r2。
function [th3,th4,th5]=f5link_int(r1,R2,R4,r5)
% Program 7.1 solving eqs 7.11-7.17
% The 5 link system consists of 2 gears with one
% holding link(r5), except the ground(r1)
% Find the initial positions of the 5-link system
% Input:
% r1,r5: the length of ground and the 5th links.
% R2,R4: radius of the gear pair
%
% Output:
% th3,th4,th5: angles of link 3,4 & 5, degrees
% Example: [th3,th4,th5]=f5link_int(8, 3, 3.5, 6)
d2r=pi/180;
r3=R2+R4;
r34=r3+R4;
cos5=(r34*r34-r5*r5-r1*r1)/(2*r1*r5);
cos3=(r1+r5*cos5)/r34;
th50=acos(cos5);
th30=acos(cos3);
th3=th30/d2r;th4=th3;th5=th50/d2r;
執行例:
>> [th3,th4,th5]=f5link_int(8, 3, 3.5, 6)
th3 = 36.8699
th4 = 36.8699
th5 = 90
由初始角度公式7.6:
(θ2-θ2i)-(R4/R2)(θ4-θ4i)=[1+(R4/R2)(θS-θSi)] (7.6’)
由於θ2為輸入值,故其初始值可以設為0,即θ2i=0。且R4/R2 = 3.5/3 =7/6,其他齒輪組的初始角度可由程式得到:
θS=90°
θSi=θ3i=36.8699°
θ4i=36.8699°
將上述值代入公式7.6,初始值公式轉為:
(1+7/6)(θ3 - 36.8699) = 2 + 7/6(θ4 - 36.8699) 7.18
將相關參數代入公式7.12及7.13,得:
6.5cosθ3 + 3.5cosθ4 - 6cosθ5 = 8
6.5sinθ3 + 3.5sinθ4 - 6sinθ5 = 0 7.19
由於θ2=60度,故三個未知數與三聯立方程式應可得解。但由於過程較為複雜,讀者可試用疊代法,以程式求解。本題正解為:
θ2=60.0000
θ3= 52.1875
θ4= 13.8419
θ5= 95.8522
範例7.2
如同範例7.1之情況,其五桿之相關尺寸參看圖7.6,r=[8 3 6.5 3.5 6]cm,對應角θ=[0 60.0000 47.1166 20.6388 92.8391],即θ2=60度。設輸入桿2之角速度ω2為10 rad/s CCW,試利用公式7.6、7.12及7.13進行分析。
[解] :這是延續前例求得相關角度後,再進一步計算其對應之角速度之例子。設γ= r4/r2,初值分別θ30、θ40,則公式7.6、7.12及7.13可改寫如下:
r3cosθ3 +r4cosθ4 -r5cosθ5 -r1 =0
r3sinθ3 +r4sinθ4 -r5sinθ5 =0
(1 + γ)(θ3-θ30) =θ2 +γ(θ4-θ40) (7.28)
為求得各桿之角速度,可先將上式之兩邊對時間t微分:
-r3sinθ3ω3 -r4sinθ4ω4 +r5sinθ5ω5 =0
r3cosθ3ω3 +r4cosθ4ω4 -r5cosθ5ω5 =0
(1 + γ)ω3 -γω4 =ω2 (7.29)
公式7.29可直接用聯立方程式求解,亦可利用矩陣表示如下:
[ -r3sinθ3 -r4sinθ4 r5sinθ5] [ ω3] [0 ]
[ r3cosθ3 r4cosθ4 -r5cosθ5] [ ω4] = [0 ] (7.30)
[ (1 +γ) -γ 0 ] [ ω5] [ω2]
公式7.30之矩陣亦可以簡化為:AW=C之型式。再以MATLAB指令W=A\C解出桿3、4、5之角速度。程式內容參見f5link()。其中之呼叫參數說明如下:
function [omega,theta,incta]=f5link(r1,R2,R4,r5,theta2,omega2)
輸入:r1、r5為第一(地桿)及第五桿之長度。
R2、R4為成對之齒輪半徑。
omega2為桿2之驅動角速度,rad/s。
theta2各桿2之對應角度。
輸出:omega為桿2、3、4、5之角速度。
theta為桿2、3、4、5之水平角度。
Incta為桿3與桿4成一直線時,桿3、4、5之初始角度。
程式內容
function [omega,theta,incta]=f5link(r1,R2,R4,r5,tha2,w2)
% Program 7.2
% Solve the angular velocities of a 5-link system
% Input:
% r1,r5: the length of ground and the 5th links.
% R2,R4: radius of the gear pair%
% tha2: angular position of link 2, degrees
% w2: angular velocity of link 2, rad/s
% Output:
% omega:the ang. velocitis of links, rad/s
% theta:the angles of links, degrees
% incta:initial positions of links, degrees
% omega=[omega3 omega4 omega5], in rad/s
% Example [omega,theta,incta]=f5link(8,3,3.5,6,60,10)
d2r=pi/180;th2=tha2*d2r;
r3=R2+R4;
if r3+r5<=r5,
theta='Not available';
incta=0;
return
end
r34=r3+R4;
cos5=(r34*r34-r5*r5-r1*r1)/(2*r1*r5);
cos3=(r1+r5*cos5)/r34;
th50=acos(cos5);
th30=acos(cos3);th40=th30;
incta=[th30 th40 th50]/d2r;
%============================================
% To solve the angular position of each links
rr=R4/R2;
func_1=1; func_2=1;
% Force next WHILE statement to be true
th5=th50;th4=th40;
while abs(func_1)>0.01 | abs(func_2)>0.01,
% Evaluate loop equations
th3=th30+(th2+rr*(th4-th40))/(1+rr);
func_1=r3*cos(th3)+R4*cos(th4)-r5*cos(th5)-r1;
func_2=r3*sin(th3)+R4*sin(th4)-r5*sin(th5);
F=[-func_1; -func_2];
% Evaluate partial derivatives
A=[-r3*sin(th3)*rr-R4*sin(th4) r5*sin(th5);...
r3*cos(th3)*rr+R4*cos(th4) -r5*cos(th5)];
% Solve 2 equations in 2 unknowns with Cramer's rule
delta=A\F;
% Make new guess for both theta3 and theta4
th4=th4+delta(1);
th5=th5+delta(2);
end;
theta=[0 th2 th3 th4 th5]/d2r;
%============================================
% Calculate the angular velocities of links
% Set up the 3x3 maxtrix A
A=[-r3*sin(th3) -R4*sin(th4) r5*sin(th5);...
r3*cos(th3) R4*cos(th4) -r5*cos(th5);...
1+rr -rr 0];
C=[0 0 w2]';
W=A\C; %Matrix division, or solution of AW=C
omega=[w2,W'];
執行例一:r1=8 cm、R2=3 cm、R4=3.5 cm、r5= 6cm,θ2= 60度,ω2=10 rad/s
>> [w,theta,incta]=f5link(8,3,3.5,6,60,10)
w = 10.0000 2.7194 -3.5211 1.8456
theta = 0 60.0000 52.1875 13.8419 95.8522
incta = 36.8699 36.8699 90.0000
故ω3=2.7194 rad/s,ω4= -3.5211 rad/s, ω5= 1.8456 rad/s
執行例二:r1=50 cm、R2=12 cm、R4=14 cm、r5= 50cm,θ2= 30度,ω2=10 rad/s,則:
>> [omega ,theta,incta]=f5link(50,12,14,50,30,10)
omega = 10.0000 2.4549 -4.0123 0.4351
theta = 0 30.0000 73.5832 54.0023 133.5048
incta = 66.4218 66.4218 132.8436
故ω3= 2.4549 rad/s,ω4=-4.0123 rad/s, ω5= 0.4351 rad/s
本程式中,實際上綜合f5link_init()函式之內容,並進行作位置解,將公式7.18及7.19利用疊代法求得各桿之對應角度。其後再利公式7.30之矩陣除法求得各桿之角速度。在求解過程中,桿2之角度及角速度均必須為已知值。
習題7.10
試就範例7.1,撰寫一MATLAB程式以求得θ3、θ4、θ5之適當解。
[解]:
由範例一之三個聯立方程式改為通式,並設γ= R4/R2,初值分別θ30、θ40,則方程式可改寫如下(7.28):
r3cosθ3 +r4cosθ4 -r5cosθ5 -r1 =0
r3sinθ3 +r4sinθ4 -r5sinθ5 =0
(1 + γ)(θ3-θ30) =θ2 +γ(θ4-θ40) (1)
將公式(1)c改變如下:
θ3 = θ30 + θ2/(1+γ) + [γ/(1+γ)](θ4 - θ40)
上式中,θ2為輸入,其餘僅θ4為變數,故若對θ4微分應可得:
d(θ3)/d(θ4) = [γ/(1+γ)] (2)
利用疊代法以泰勒級數展開式求解,首先將公式(1)之前兩式設為兩個函數f1(θ4,θ5),f2(θ4, θ5) ,或:
f1(θ4,θ5)=r3cosθ3 +r4cosθ4 - r5cosθ5 -r1 =0
f2(θ4,θ5)=r3sinθ3 +r4sinθ4 - r5sinθ5 =0
上兩函數之最終值均應等於零,其對應之θ4,θ5值即為答案。首先可以給兩個初估值,再利用泰勒展開式求其誤差Δθ4,Δθ5,即:
f1(θ4,θ5)=df1/d(θ4)Δθ4 +df1/d(θ5)Δθ5
f2(θ4,θ5)=df2/d(θ4)Δθ4 +df2/d(θ5)Δθ5 (3)
為簡化起見僅取其第一項。而θ3因公式(2)之關係與之θ4變數可作轉換,在此僅列出二項變數。
公式(3)可化為矩陣型式以求解:
[df1/d(θ4) df1/d(θ5)] [Δθ4 ] = [-f1]
[df2/d(θ4) df2/d(θ5)] [Δθ5 ] [-f2] (4)
求得Δθ4, Δθ5之後可以得到新值,如此循環運算直到獲得合理答案為止。
公式(3)與(4)中之偏微分係數可以計算如下:
df1/d(θ5)=r5sinθ5
df2/d(θ5)=-r5cosθ5
df1/d(θ4)=d{r3cosθ3 +r4cosθ4 - r5cosθ5 -r1 }/dθ4
=-r3sinθ3(1+γ)/γ-r4sinθ4
df2/d(θ4)=r3cosθ3(1+γ)/γ+r4cosθ4
MATLAB之程行內容如下:
function [angle, init]=exP7_9(r,theta2,theta4,theta5)
%
% Find the position for 5-Link mechanism that contains one pair of gears
% in mesh using Tayler's series
% Input:r: length of five links
% theta2: input angle in degrees
% theta4, theta5:gusessing angles
% Output: angle: all angles in degree
% init: initial angles
% Example: [angles,init]=exP7_9([50 12 36 14 50],60,0,100)
% --Program designed by Din-sue Fon
d2r=pi/180;
gama=(r(3)-r(2))/r(2);rr=(1+gama)/gama;
% Find the initial value for theta3 & theta4
r34=r(3)+r(4);
cos5=(r34*r34-r(5)*r(5)-r(1)*r(1))/(2*r(1)*r(5));
cos3=(r(1)+r(5)*cos5)/r34;
th50=acos(cos5);
th30=acos(cos3);
th40=th50-th30;
init=[th30 th40 th50]/d2r;
func_1=1; func_2=1; % Force next WHILE statement to be true
th2=theta2*d2r;th5=theta5*d2r;th4=theta4*d2r;
while abs(func_1)>0.01 | abs(func_2)>0.01,
% Evaluate loop equations
th3=th30+(th2+gama*(th4-th40))/(1+gama);
func_1=r(3)*cos(th3)+r(4)*cos(th4)-r(5)*cos(th5)-r(1);
func_2=r(3)*sin(th3)+r(4)*sin(th4)-r(5)*sin(th5);
F=[-func_1; -func_2];
% Evaluate partial derivatives
A=[-r(3)*sin(th3)*rr-r(4)*sin(th4) r(5)*sin(th5);...
r(3)*cos(th3)*rr+r(4)*cos(th4) -r(5)*cos(th5)];
% Now solve 2 equations in 2 unknowns with Cramer's rule
delta=A\F;
% Make new guess for both theta3 and theta4
th4=th4+delta(1);
th5=th5+delta(2);
end;
angle=[th2 th3 th4 th5]/d2r;
執行例一:
>> [angle,in]=exP7_9([8 3 6.5 3.5 6],60,0,100)
angle =60.0000 47.0356 20.6090 92.8499
in = 36.8699 53.1301 90.0000
得到的角度如下:
θ2=60.0000
θ3=47.0356
θ4=20.6090
θ5=92.8499
執行例二:輸入角θ2為30,r=[50 12 36 14 50],則
>> [angles,init]=exP7_9([50 12 36 14 50],30,0,100)
angles = 30 63.819 50.736 120.35
init = 60 60 120
得到的角度如下:
θ2=30.0000
θ3=63.819
θ4=50.736
θ5=120.35
其初始角分別為
θ30=60
θ40=60
θ50=120
習題7.11
試就範例7.1之五連桿,其尺寸為r=[8 3 6.5 3.5 6]cm,當θ2=60。時其對應角為θ=[0 60 47.1 20.6 92.8]度。復由範例7.2得其對應角速度為ω=[0 10 2.634 -3.679 1.336] rad/s(正值為CCW),設ω2=10 rad/s CCW為定值,試撰寫一MATLAB程式以求得α3、α4、α5之適當解。
[解]:
將公式7.28對時間t再微分,改寫之得:
-r3sinθ3α3-r4sinθ4α4+r5sinθ5α5=r3cosθ3ω3²+r4cosθ4ω4²-r5cosθ5ω5²
r3cosθ3α3+r4cosθ4α4-r5cosθ5α5=r3sinθ3ω3²+r4sinθ4ω4²-r5sinθ5ω5²
(1+γ)α3-γα4 = 0
[-r3sinθ3 -r4sinθ4 r5sinθ5] [α3] [f1]
[ r3cosθ3 r4cosθ4 -r5cosθ5] [α3] = [f2]
[ 1+γ -γ 0 ] [α4] [ 0]
:
MATLAB程式撰寫如下:
function [alpha]=EX7_10(r,theta,omega)
% P7_2
% Problem No. 2 Find the angular velocities of the 5-link system
% theta: angles for each link(include the 1st link), in degrees
% omega:[omega1 omega2 omega3 omega4 omega5]
% Example [omega]=EX7_10([50 12 36 14 50],[0 30 63.819 50.736 120.35],[0 10 1.3198 -3.0203 0.22948])
%
d2r=pi/180;
th=theta*d2r;
rr=(r(3)-r(2))/r(2);
ww=omega.*omega;
A=[-r(3)*sin(th(3)) -r(4)*sin(th(4)) r(5)*sin(th(5));...
r(3)*cos(th(3)) r(4)*cos(th(4)) -r(5)*cos(th(5));...
1+rr -rr 0];
F=[r(3)*cos(th(3))*ww(3)+r(4)*cos(th(4))*ww(4)-r(5)*cos(th(5))*ww(5);...
r(3)*sin(th(3))*ww(3)+r(4)*sin(th(4))*ww(4)-r(5)*sin(th(5))*ww(5);0];
W=A\F;
alpha=W';
執行例一:
r=[8 3 6.5 3.5 6],θ=[0 60 47.0 20.6 92.9],ω=[0 10 2.6316 -3.6841 1.3306] rad/s
>> [omega]=EX7_10([8 3 6.5 3.5 6],[0 60 47.0 20.6 92.9],…
[0 10 2.6316 -3.6841 1.3306])
omega = 3.2362 6.0102 16.436
故α3=2.6316 rad/s2,α4= -3.6841 rad/s2,α5= 1.3306 rad/s2
>> [omega]=EX7_10([50 12 36 14 50],[0 30 63.819 50.736 120.35],[0 10 1.3198 -3.0203 0.22948])
omega = 1.5375 2.3062 4.2759
故α3=1.5375 rad/s2,α4= 2.3062 rad/s2,α5= 4.2759 rad/s2




















